●知識グラフ全体 ，●このページを中心とした周辺知識グラフ
応用分野： 三角方程式の解き方 ， 三角関数の不等式の解き方 ， 2倍角の公式 ， 3倍角の公式 ， 三角関数　積和の公式 ， 三角関数の合成公式 ， 2直線のなす角 ， 複素数の積 ， 複素数の商 ， ド・モアブルの定理 ， cos関数の合成 ， 曲率 ， 回転行列 ， cos関数の合成（導出） ， 加法定理の証明(ベクトル編) ， 行列式の幾何学的意味 ， 加法定理の証明(ベクトル編)
問題リスト←このページに関連している問題です

加法定理

  1.   sin ( α ± β ) = sin α cos β ± cos α sin β
  2.   cos ( α ± β ) = cos α cos β ∓ sin α sin β
  3.   tan ( α ± β ) = tan α ± tan β 1 ∓ tan α tan β

（複号同順）

⇒証明へ

■解説動画

◇三角関数の動画一覧のページへ

■加法定理より派生する公式

2倍角の公式，3倍角の公式，半角の公式，和積の公式，積和の公式，合成公式

■加法定理の図形による理解

α < 90 ° ， β < 90 ° ， α + β < 90 ° ， 0 < α − β < 90 ° の場合について図形を用いて加法定理を理解する．

●和の場合

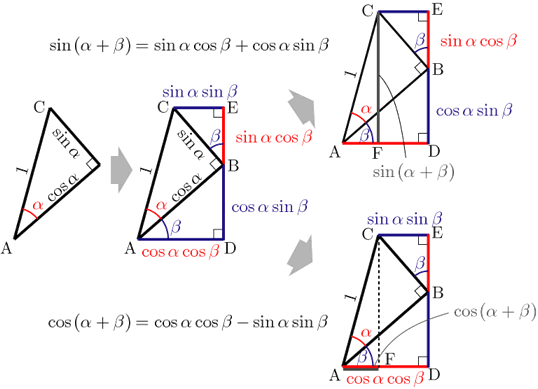この図を理解するのに参考になるページ⇒ここ

図より

sin ( α + β ) = sin α cos β + cos α sin β
cos ( α + β ) = cos α cos β − sin α sin β

となる．　

●差の場合

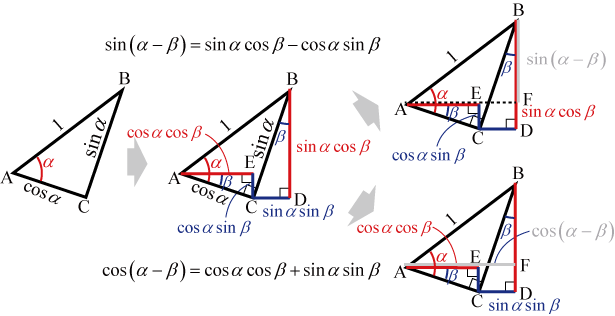この図を理解するのに参考になるページ⇒ここ


図より

sin ( α − β ) = sin α cos β − cos α sin β
cos ( α − β ) = cos α cos β + sin α sin β

となる．

よって，2つの図よりsinとcosについて加法定理が導かれた．

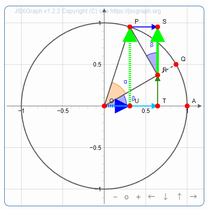
■インターラクティブな図形

下の画像をクリックしてください． 

 

■関連動画

◇三角関数の動画一覧のページへ

ホーム>>カテゴリー分類>>三角関数>>加法定理

最終更新日 2026年2月10日

[ページトップ]

金沢工業大学

利用規約，誤植や誤りなどがございましたら、こちらからご連絡ください。

google translate (English version)