対数に関する問題

1. 次の式を解け.

   • •	${\displaystyle {log}_{2}4}$　⇒ 解答

   • •	${\displaystyle {log}_{3}27}$　⇒ 解答

   • •	${\displaystyle {log}_{\frac{1}{2}}32}$　⇒ 解答

   • •	${\displaystyle {log}_2\left(\frac{1}{\sqrt{8}}\right)}$　⇒ 解答
2. 次の等式が成立することを示せ．

   ${\displaystyle {\log }_{a}b=\frac{1}{{\log }_{b}a}}$     ⇒ 解答

3. 次の値を求めよ．

   • •	${\displaystyle {log}_{6}18+{log}_{6}12}$　⇒ 解答

   • •	${\displaystyle {log}_{2}81\cdot {log}_{3}2}$　⇒ 解答

   • •	${\displaystyle {log}_9\sqrt[\text{4}]{\text{3}}+{log}_{\frac{1}{3}}9}$　⇒ 解答

   • •	${\displaystyle {log}_{2}64÷{log}_{3}27}$　⇒ 解答

   • •	${\displaystyle log{e}^2+log\frac{1}{e}+log\frac{1}{\sqrt{e}}}$　⇒ 解答

   • •	${\displaystyle {log}_{8}125-{log}_{4}10-{log}_2\left(\frac{1}{\sqrt{10}}\right)}$　⇒ 解答

   • •	${\displaystyle {log}_{\sqrt{3}}8+{log}_{2}3{log}_{9}4+{log}_{\frac{1}{3}}16}$ 　⇒ 解答

   • •	${\displaystyle \frac{{log}_{2}9+{log}_{2}3}{3}+\frac{2{log}_{2}5+{log}_{2}125}{1-{log}_{2}10}}$ 　⇒ 解答
4. 次の方程式を解け．

   • •	${\displaystyle {log}_{5}2x=-1}$　⇒ 解答

   • •	${\displaystyle {log}_2\left(x+3\right)+{log}_2\left(x-4\right)=3}$　⇒ 解答

   • •	${\displaystyle {log}_3\left(x-1\right)={log}_9\left(x+1\right)}$　⇒ 解答
5. 次の不等式を解け．

   • •	${\displaystyle {log}_2\left(x+2\right)+{log}_{2}x<3}$　⇒ 解答

   • •	${\displaystyle {log}_2\left(x-1\right)+{log}_{4}2<0}$　⇒ 解答

   • •	${\displaystyle {\left({\log }_{\frac{1}{2}}x\right)}^2-{\log }_{\frac{1}{2}}x<2}$　⇒ 解答

   • •	${\displaystyle {log}_{3}9\cdot {log}_{\frac{1}{3}}4\leqq {log}_{9}x\leqq {log}_{\frac{1}{3}}4+{log}_{3}2}$　⇒ 解答

   • •	${\displaystyle \frac{1}{3}{log}_2{x}^3+\frac{1}{2}{log}_2\left(x^2+4x+4\right)\leqq 3}$ 　⇒ 解答

   • •	${\displaystyle {\left({log}_{3}x\right)}^2-5{log}_{3}9x<-4}$ 　⇒ 解答
6. 次の問に答えよ．

   • ${\displaystyle 3^{50}}$は何桁の数か求めよ．ただし，${\displaystyle {log}_{10}3=0.4771}$である．    ⇒ 解答

   • ${\displaystyle 3^{50}}$の最上位の数を求めよ．ただし，${\displaystyle 1}$から${\displaystyle 10}$までの常用対数表は用いてよい．    ⇒ 解答

   • ${\displaystyle 5^{65}}$の桁数を求めよ．また，最上位の数は何か．ただし，${\displaystyle {\log }_{10}2=0.301}$ ，${\displaystyle {\log }_{10}3=0.477}$，${\displaystyle {\log }_{10}7=0.845}$ とする．    ⇒ 解答

   • ${\displaystyle {\left(\frac{1}{6}\right)}^{75}}$ は小数第何桁に初めて$0$でない数字が現れるか．また，その$0$でない数を求めよ．ただし，${\displaystyle {\log }_{10}2=0.301}$ ，${\displaystyle {\log }_{10}3=0.477}$，${\displaystyle {\log }_{10}7=0.845}$ とする．    ⇒ 解答

7. 次の式のグラフを描け．

   • •	${\displaystyle y={log}_{2}x}$　⇒ 解答

   • •	${\displaystyle y={log}_{\frac{1}{2}}x}$　⇒ 解答

   • •	${\displaystyle y={log}_{3}x}$　⇒ 解答

   • •	${\displaystyle y={log}_2\left(x-1\right)}$　⇒ 解答

   • •	${\displaystyle y={log}_{2}x+1}$　⇒ 解答

   • •	${\displaystyle y={log}_2\left(x+2\right)-1}$　⇒ 解答

   • •	${\displaystyle y={log}_2\left(x+1\right)+2}$　⇒ 解答

   • •	${\displaystyle y={log}_{2}2x}$　⇒ 解答

   • •	${\displaystyle y={log}_2\left(2x+1\right)+1}$　⇒ 解答

   • •	${\displaystyle y={log}_2\left(3x+1\right)+2}$　⇒ 解答
8. 次の問に答えよ．

   • 
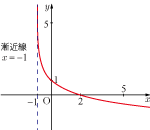
     図は $x=-1$ を漸近線とする対数関数のグラフである．グラフを表す関数の式を求めよ．     ⇒解答

   • ${\displaystyle y=2+3{log}_{\frac{1}{2}}\left(4x+2\right)}$のグラフは${\displaystyle y={log}_{2}x}$をどのように変形したものか述べよ．またそのグラフを描け．     ⇒解答

 

ホーム>>カテゴリー分類>>指数/対数>>対数に関する問題

最終更新日： 2024年2月20日